|
Specifically, at n = 0 and f (0) = 1 there is
Introducing the condition of symmetry of the system in the form
we get an equation, containing an unknown function
From geometric
considerations it follow that the limit of the
relationship of the band of frequencies to the average frequency of
rhythm, with the leaning of the rhythm to infinity, is equal
Furthermore, let us assume
where F (−n) = k (n) F (n) (8) To detect the source of information at frequency f (0), the content and statistical nature of which was previously unknown, it is necessary that search be conducted at least on two sliding frequencies f (−n) and f (n). The relationship between these frequencies is determined by equation (6). Furthermore execution of the following conjunction is necessary:
where An and A−n — the same type information taken in frequencies |
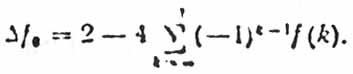 (4)
(4)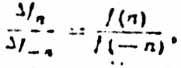 (5)
(5)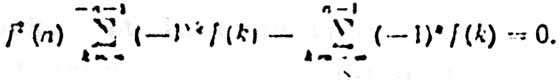 (6)
(6) (7)
(7)